Intervalli (musiikki)

Intervalli ( lat. intervallum - rako, etäisyys; ero, erilaisuus) musiikissa - kahden musiikin äänen suhde niiden korkeuden mukaan [1] . Eurooppalaisessa musiikin teoriassa koko ääni on vuosisatojen ajan ollut musiikillisten intervallien laskemisen mitta, johon nähden sekä pienemmät (esimerkiksi puolisävel , neljännessävel) että jotkut suuremmat (esim. ditoni , puolisäveli , tritone ) välit määriteltiin. Eurooppalaisen perinteen pienintä musiikkiväliä pidetään puolisävelenä . Puolisäveltä pienempiä intervalleja kutsutaan mikrointervalleiksi . Konsonantti- ja dissonanttivälit ovat harmonian tärkeimpiä elementtejä .

Intervallin kaksi puolta

Toisaalta intervalli voidaan esittää matemaattisena ( akustisena ) arvona, joka ilmaisee kahden luvun - siihen sisältyvien äänten pääharmonisten taajuuksien - suhteen . Teoreettisesti "oikeilla" eli luonnollisimmilla aikaväleillä taajuudet tulee suhteuttaa pieninä kokonaislukuina, esimerkiksi 3:2 kvinttiä varten [2] [3] . Tasaisessa luonteessa suhteet poikkeavat hieman "oikeista" (esim. 1,498307 3:2:n sijaan). Joskus suhteen sijaan käytetään taajuuksien logaritmien eron ekvivalenttiarvoa ( senttiä 3:2:lle). Intervallin absoluuttinen matemaattinen arvo määritetään mekaanisilla ( monoskordilla tms.) tai elektronisilla (sovelletun tietokoneohjelman avulla) mittauksilla. $f_{B}/f_{A}$ $n=1200\log _{2}f_{B}-1200\log _{2}f_{A}=1200\log _{2}(f_{B}/f_{A})$ $n=702.0$

Toisaalta intervalli on nimenomaan musiikillisen logiikan luokka, joka näkyy jo musiikillisessa terminologiassa. Esimerkiksi termi quinta viittaa diatonisen asteikon viiden askeleen käsitteeseen (viides askel [quinta vox] lasketaan intervallin perustasta, jota kutsutaan "primaksi"). Nuotinkirjoituksen tarjoamasta kontekstista (kirjain, lineaarinen jne.) johdetaan intervallin musiikki-looginen arvo.

Intervalli matemaattisena (akustisena) suureena ei voi olla yksiselitteisesti assosioitunut nuottimusiikkiin. Esimerkiksi klassisen harmonian opin merkintä eis-a ("mi terävä" - "la") tulkitaan kromaattiseksi intervalliksi (reduced quart , tarkoittaa mi-terävän erottelukykyä f-terävässä), enharmoninen yhtä suuri kuin duuri. Kolmasosa yhtenäisestä luonteesta , toisessa yhteydessä se voi tarkoittaa sekä Pythagoraan ditonia että puhtaan asteikon suurta kolmannesta (esimerkiksi 1500-luvun italialaisessa madrigalissa ). Intervalli, joka on merkitty fis-a:ksi ("F-sävy" - "la") C-durin sävelsävyssä (C-duuri), voidaan katsoa tasaisesti temperoidun systeemin pienenä kolmanneksena ja kromaattisen tetrakordin . kreikkalaisten keskuudessa - puoli-toratonina tai puoliditonina jne.

Koska nuottikirjoitus kiinnittää vain intervallien musiikillisen (eikä matemaattisen) puolen, kysymys tämän tai tuon musiikin ( etenkin vanhan musiikin ) äänen akustisesta "aitoisuudesta" ei ole järkevä. Intervallin "numeron" ja " harmonisen logiikan" välisen suhteen epäselvyys avaa tilaa nuottimusiikin musikologisille ja esittäville tulkinnoille.

Intervallien luokitus

Intervallin alempaa ääntä kutsutaan pohjaksi, ylempää ääntä topiksi. Intervallit luokitellaan:

1. Ottamalla: samanaikainen (harmoninen tai "pystysuuntainen", intervalli) tai peräkkäinen (melodinen tai "vaaka", intervalli) [4] .

2. Niihin sisältyvien portaiden määrällä (määrällä) . Intervallin vaiheiden lukumäärää osoittava numero on myös lyhenne kyseiselle ajanjaksolle. Intervalleja primasta oktaaviin kutsutaan yksinkertaisiksi , oktaavin yläpuolella oleviksi . Yhdistelmävälit perivät yksinkertaisten ominaisuudet (esimerkiksi ei mitään, kuten sekuntia, voi olla suuria ja pieniä) [5] . Kaksioktaavia (quintdecim) leveämpiä intervalleja ei perinteisesti oteta huomioon musiikin perusteoriassa.

3. "laadulla". Välin "laatu" määritetään sanoilla "suuri" (lyhennetty b. ), "pieni" ( m. ), "puhdas" ( h. ), "lisätty" ( uv. ), "alennettu" ( min. . ), "kaksi kertaa suurentunut" ( dv. uv. ) ja "kaksinkertaistettu" ( dv. um. ), selventäen intervallin kvantitatiivista ominaisuutta.

Termit "suuri" ja "pieni" viittaavat sekuntien, kolmannesten, kuudenten ja seitsemäsosien aikaväleihin.
Termi "puhdas" viittaa priman, kvarttien, kvinttien ja oktaavien väleihin.

4. Eufonian asteen mukaan. Antiikista duuri-molli tonaalisuuden aikakauteen intervallit jaettiin myös sen mukaan, kuinka saumattomasti korva ne havaitsee (katso lisätietoja artikkelista Konsonanssi ja dissonanssi ). Erilaisissa historiallisissa luokitteluissa teoreetikot erottivat (järjestyksessä eufonisimmasta dissonanttimpaan) "täydelliset konsonanssit", "epätäydelliset konsonanssit", "epätäydelliset dissonanssit", "täydelliset dissonanssit" ja muut arvioivat termit.

Suuremmat ja pienemmät intervallit

Alkeis -duuri-molli musiikin teoriassa termit "pienennetyt" ja "korotetut" intervallit tarkoittavat muutosta intervallin sävyjen lukumäärässä, kun taas askelmien määrä pysyy ennallaan [6] .

Lisätty - päätyyppiä intervalli (puhdas tai suuri) kasvatetaan puolisävel.
Alennettu - päätyyppiä intervalli (puhdas tai pieni) lasketaan puolisävelellä (paitsi "prima").
Kaksinkertainen lisätty - päätyyppiä intervalli (puhdas tai suuri) kasvatetaan kokonaisella äänellä.
Kaksinkertaisesti pienennetty - päätyyppiä (puhdas tai pieni) pienennetään kokonaisella äänellä (paitsi "prima" ja "minor second").

Esimerkkejä:

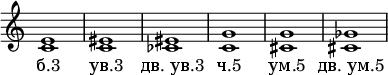
$\new Staff \with {\remove "Time_signature_engraver"} { < c' e' >1 < c' eis' > < ces' eis' > < c' g' > < cis' g' > < cis' ges' > } \addlyrics {"b.3" "sw.3" "dv.v.3" "ch.5" "min.5" "dv.w.5"}$

Musiikissa, jossa ei ole duuri-molli tonaliteettia (esimerkiksi New Wienin koulukunnan säveltäjien dodekafoniassa ), termit "vähennetty" ja "lisätty" menettävät merkityksensä, ja termiä "puhdas" käytetään vain akustisen puhtauden tunne (katso Pure tuning ).

Luettelo musiikin intervalleista

Seuraavat taulukot havainnollistavat intervallityyppejä sellaisina kuin ne on tavallisesti kuvattu 1900-luvun musiikin perusteorian käsikirjoissa (esimerkiksi B. Aleksejevin ja A. Myasoedovin ETM:ssä [7] ).

Vaiheiden lukumäärä	Nimi	Erilaisia	Äänien määrä	Nimitys
Yksinkertaiset intervallit
Esimerkkejä yksinkertaisista harmonisista intervalleista: $\new Staff \with {\remove "Time_signature_engraver"} { < c' c' >1 < c' des' > < c' d' > < c' es' > < c' e' > < c' f' > < c' fis' > < c' ges' > < c' g' > < c' aes' > < c' a' > < c' bes' > < c' b' > < c' c' > } \addlyrics {"ch.1" "m.2" "b.2" "m.3" "b.3" "ch.4" "sw.4" "um.5" "ch.5" "m .6" "b.6" "m.7" "b.7" "ch.8"}$
yksi	Prima	puhdas	0 ( yhdessä )	osa 1
2	Toinen	pieni iso	0,5 ( puolisävel ) 1 ( koko ääni )	m.2 b.2
3	Kolmas	pieni iso	1,5 ( puoli ditoni ) 2 ( ditoni )	m.3 b.3
neljä	Quart	verkkoa suurennettu	2,5 3 ( triton )	osa 4 uv.4
5	Quint	vähennetty netto	3 (tritoni) 3.5	mieli.5 h.5
6	Kuudes	pieni iso	4 4.5	m.6 b.6
7	Seitsemäs	pieni iso	5 5.5	m.7 b.7
kahdeksan	Oktaavi	puhdas	6	osa 8
Yhdistelmävälit
Esimerkkejä yhdistetyistä harmonisista intervalleista: $\new Staff \with {\remove "Time_signature_engraver"} { < c' des'' >1 < c' d'' > < c' es'' > < c' e'' > < c' f'' > < c' fis'' > < c' ges'' > < c' g'' > < c' aes'' > < c' a'' > < c' bes'' > < c' b'' > < c ' c''' > } \addlyrics {"m.9" "b.9" "m.10" "b.10" "ch.11" "sw.11" "min.12" "ch.12" "m.13" "b.13" "m.14" "b.14" "ch.15"}$
9	Nona (toinen + h.8)	pieni iso	6.5 7	m.9 b.9
kymmenen	Decima (kolmas + osa 8)	pieni iso	7.5 8	m.10 b.10
yksitoista	Undecima (kvarttia + osa 8)	verkkoa suurennettu	8.5 9	osa 11 uv.11
12	Duodecima (viides + osa 8)	vähennetty netto	9 9.5	mieli.12 h.12
13	Tertsdecima (seksta + osa 8)	pieni iso	10 10.5	k.13 b.13
neljätoista	Quartdecima (septima + osa 8)	pieni iso	11 11.5	k.14 b.14
viisitoista	Quintdecima (oktaavi + h.8)	puhdas	12	osa 15

Yksinkertaiset intervallit, myös kromaattiset [8]

Vaiheiden lukumäärä	Nimi	Laatu	Äänien määrä	Nimitys	Quint askeleet
yksi	Prima	puhdas	0	osa 1	0
yksi	Prima	laajennettu	0.5	SW.1	7
2	Toinen	pieni	0.5	m.2	5
		iso	yksi	b.2	2
		laajennettu	1.5	SW.2	9
		vähennetty	0	mieli.2	12
3	Kolmas	pieni	1.5	m.3	3
		iso	2	b.3	neljä
		vähennetty	yksi	mieli.3	kymmenen
		laajennettu	2.5	SW.3	yksitoista
neljä	Quart	puhdas	2.5	osa 4	yksi
		laajennettu	3	SW.4	6
		vähennetty	2	mieli.4	kahdeksan
5	Quint	puhdas	3.5	osa 5	yksi
		vähennetty	3	mieli.5	6
		laajennettu	neljä	SW.5	kahdeksan
6	Kuudes	pieni	neljä	m.6	neljä
		iso	4.5	b.6	3
		vähennetty	3.5	mieli.6	yksitoista
		laajennettu	5	SW.6	kymmenen
7	Seitsemäs	pieni	5	m.7	2
		iso	5.5	b.7	5
		laajennettu	6	SW.7	12
		vähennetty	4.5	mieli.7	9
kahdeksan	Oktaavi	puhdas	6	osa 8	0
kahdeksan	Oktaavi	vähennetty	5.5	mieli.8	7

12 - portaisessa tasatemperamenttijärjestelmässä , josta on tullut eurooppalaisen musiikin pääjärjestelmä 1700-luvulta lähtien, intervallin muodostavien äänien taajuuksien suhde lasketaan seuraavasti , missä on äänien lukumäärä (katso yllä oleva taulukko) . $2^{N/6}$ $N$

Valitukset

Intervallin inversio on sen pohjalla olevan äänen liikettä, oktaavi ylös tai intervallin yläosa - oktaavi alas. Käänteisenä intervallin laatu kääntyy päinvastaiseksi: suuresta tulee pieni, suurennettu väli pienenee, kaksinkertainen intervalli pienenee kaksinkertaiseksi ja päinvastoin. Puhdas väli pysyy puhtaana. Yksinkertaisilla intervalleilla päätyypin intervallin ja sen inversion digitaalisten merkintöjen summa on aina yhtä suuri kuin yhdeksän.

Perusvälit	Käänteinen intervalli
Prima (1)	Oktaavi (8)
Toinen (2)	Septima (7)
Kolmas (3)	Sexta (6)
Quart (4)	Quinta (5)
Quinta (5)	Quart (4)
Sexta (6)	Kolmas (3)
Septima (7)	Toinen (2)
Oktaavi (8)	Prima (1)

Jos yhdistelmäintervalli on käännettävä, sen molemmat äänet siirretään oktaaville (ylä - alas, ala - ylös) tai toinen niistä kahteen oktaaviin, kun taas molempien intervallien digitaalisten merkintöjen summa on aina yhtä suuri kuin kuusitoista.

Perusvälit	Käänteinen intervalli
Nona (9)	Septima (7)
Decima (10)	Sexta (6)
Undecima (11)	Quinta (5)
Duodecyma (12)	Quart (4)
Terzdecima (13)	Kolmas (3)
Quartdecima (14)	Toinen (2)
Quintdecima (15)	Prima (1)

Korotettu oktaavi, jota pidetään myös yhdistelmävälinä, antaa pienentyneen oktaavin kierrossa.

Muistiinpanot

↑ Nazaikinsky E. V. Interval Arkistokopio 16. huhtikuuta 2018 Wayback Machinessa // Great Russian Encyclopedia. Osa 11. - M., 2008. - S. 435.
↑ Kotimaisessa musiikkitieteessä intervallin numeerista suhdetta kutsutaan usein väärin " osuudeksi ". Esimerkiksi E.V. Gertsman: "… kuulostava tulee ilmaista numerolla… voidaan turvallisesti esittää terveitä suhteita tietyillä numeerisilla suhteilla. Mutta koska epätasaiset määräsuhteet esitetään erityyppisillä suhteilla, äänien väliset etäisyydet (intervallit) voidaan tallentaa samalla tavalla, eli moninkertaisina, epimoraalisina, epimeerisinä ja muina suhteina” (Pythagoran musicology. SPb., 2003, s. 280-281. ).
↑ Yksityiskohtaisia tietoja aritmeettisista termeistä "suhde" ja "suhde" löytyy aritmeettisista oppikirjoista, esimerkiksi A. S. Kiselevin oppikirjan " Systematic Arithmetic Course" 4. joulukuuta 2016 päivätyn arkistokopion luvusta Wayback Machine .
↑ Termit "vaakaväli" ja "pystyväli" tulivat käyttöön 1900-luvun viimeisinä vuosikymmeninä, katso esimerkiksi: Kholopov Yu. N. Harmony. Teoreettinen kurssi. M., 1988, s. 22. 1950-luvulla kirjoitetuissa musiikkiteorian tähän asti suosituissa oppikirjoissa. - I. V. Sposobina (1951), V. A. Vakhromeev (1956) sekä G. A. Fridkinin (1957) "Musiikkilukutaidon käytännön oppaassa" - vain termit (vastaavasti) "melodinen intervalli" ja " harmoninen intervalli".
↑ Intervalli // Kazakstan. Kansallinen tietosanakirja . - Almaty: Kazakstanin tietosanakirjat , 2005. - T. II. — ISBN 9965-9746-3-2 . (Venäjän kieli) (CC BY SA 3.0)
↑ Alekseev, Myasoedov, 1986 , s. 69.
↑ Alekseev, Myasoedov, 1986 , s. 67, 70.
↑ Bityukov Sergei. 13 ääntä ja intervalleja. Heidän käsityksensä ja nimeämisensä. Poikkeaman ja modulaation nauhat (venäjäksi) ? . Habr (7. elokuuta 2021). Haettu 12. elokuuta 2021. Arkistoitu alkuperäisestä 12. elokuuta 2021. (määrätön)

Kirjallisuus

Alekseev B., Myasoedov A. Intervallit // Musiikin perusteoria. - M . : Musiikki, 1986. - S. 64-78. - 240 s.
Intervalli // Musical Encyclopedia. - M . : Neuvostoliiton tietosanakirja, 1974. - T. 2. - S. 544-545. - 960 s.
Solovjov N.F. Interval // Encyclopedic Dictionary of Brockhaus and Efron : 86 osassa (82 osaa ja 4 lisäosaa). - Pietari. , 1890-1907.
Fridkin G. Käytännön opas musiikilliseen lukutaitoon. - M.: Muzgiz, 1962

Linkit

Hugo Riemannin intervallitaulukot
Välitaulukko 365 (välien nimet ja niiden käännökset eivät ole normatiivisia)

Sanakirjat ja tietosanakirjat	Hienoa norjalaista Iso venäläinen Brockhaus ja Efron Brockhaus ja Efron Musikaali Riemann Britannica (verkossa) Musiikin ja muusikoiden sanakirja Universalis
Bibliografisissa luetteloissa	BNF : 11940596x GND : 4162149-9 J9U : 987007555760905171 LCCN : sh85089007 NKC : ph120909

Musiikki intervallit
Yksinkertainen	Prima Toinen Kolmas Quart Quint Kuudes Seitsemäs Oktaavi
Komposiitti	Nona Decima Undecima duodekyma Terzdecima Quartdecima Quintdecima
Mikrointervallit	Skisma Diaskismi Pilkku Diez Cent Millioktaavi
Erityinen	Koko sävy Puolisävelaskel Limma Apotoma Deaton Puoli Ditonia Triton Wolf Quint